일반적으로 구조적 데이터의 특정한 특성은 데이터의 4가지 수준 중 하나로 분류된다.
- 명목수준(nominal level)
- 서열수준(ordinal level)
- 등간수준(interval level)
- 비율수준(ratio level)
아래로 내려갈 수록 더 많은 구조를 얻고 따라서 분석으로 더 많은 결과를 얻게 된다. 각 수준은 데이터의 중심을 측정할 때 자체적으로 허용되는 관행을 따른다. 일반적으로 중앙값/평균을 중심의 형식으로 생각하는 경향이 있지만, 이것은 특정 유형의 데이터에만 해당된다.
명목수준
명목수준은 순수하게 이름이나 범주로 설명되는 데이터로 구성된다. 성별, 국적, 생물의 종, 맥주 효모 균주 등이 포함된다. 숫자로 기술되지 않으므로, 정성적이다.
정성적이기 때문에 당연히 더하기나 나누기 같은 정량적 수학연산을 수행할 수 없고, 의미를 전달할 수 없다.
허용된 수학연산
다음 두 가지 예에서와 같이 기본적인 equality와 set membership 함수를 제외하고는 명목 수준 데이터로는 수학 연산을 할 수 없다.
- 기술 기업가는 기술 산업에 종사하는 것과 동일하지만, 그 반대로 기술 산업에 종사하는 것이 기술 사업가는 아니다.
- 정사각형은 직사각형으로 묘사될 수 있지만, 직사각형이 정사각형으로 묘사되지는 않는다.
중심의 측정
중심의 측정은 데이터의 경향을 설명하는 숫자다. 때로는 데이터의 균형점이라고도 한다. 일반적인 예로 평균, 중앙값, 최빈수가 있다.
명목 데이터의 중심을 찾기 위해 일반적으로 데이터셋의 최빈수(가장 일반적인 요소)를 구한다. 예를 들어 WHO 주류 소비 데이터를 살펴보면, 조사에서 가장 보편적인 대륙은 아프리카였고, continet 열의 중심에 대한 가능한 선택이다.
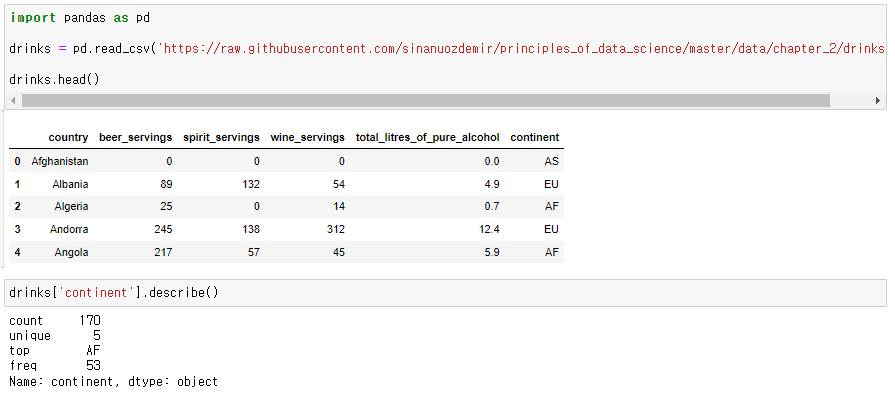
명목 수준의 데이터의 의미
명목 수준의 데이터는 본질적으로 대부분 범주화되어 있다. 일반적으로 단어를 사용해 데이터를 설명하기 때문에 국가간 번역에서 손실되거나 철자가 틀린 것이 있을 수 있다.
명목 수준의 데이터는 확실히 유용하기는 하지만, 어떤 통찰력을 얻을 수 있는 지는 주의해야 한다. 기본적인 중심 측정 방법만으로는 평균 관측치에 대한 결론을 도출할 수 없다. 이 개념은 명목 수준에서는 존재하지 않는다.
서열수준
서열 수준의 데이터는 순위를 제공하거나 다른 관측치 안에 관측치 하나를 배치할 수 있게 해준다. 그러나 관측치 간의 상대적인 차이점을 제공하지는 않는다. 즉, 관측치를 처음부터 끝까지 순서대로 나열할 수는 있지만, 실제 의미를 얻기 위해 관측치를 더하거나 뺄 수는 없다.
허용된 수학 연산
명목 수준에서 허용된 모든 수학을 적용(equality, set membership), 연산 목록에 다음을 추가할 수 있다.
- 정렬
- 비교
정렬은 데이터에 의해 제공된 자연스런 순서를 말한다.
정렬 수준에서는 어떤 나라가 당연히 다른 나라보다 좋다거나 연설의 어느 부분이 다른 연설보다 더 나빴다고 말하는 것은 합리적이지 못하다. 비교 수준에서는 이런 비교를 할 수 있다.
예를 들어 설문 조사에 7을 쓴 것이 10을 쓴 것보다 더 나쁘다고 이야기할 수 있다.
중심의 측정
서열 수준에서 중앙값은 일반적으로 데이터의 중심을 정의하는 적절한 방법이다. 그러나 서열 수준에서는 나눗셈이 허용되지 않으므로 평균은 불가능하다. 명목 수준에서 허용된 최빈수를 사용할 수도 있다.
직원들에게 "1-5점 척도로 여기에서 일하게 돼 얼마나 행복합니까?"라고 묻는 설문조사를 실시한 결과가 다음과 같다고 가정해보자.
5, 4, 3, 1, 2, 4, 4, 5, 5, 1, 2, 2, 5, 2, 3, 2, 1, 5, 5, 5, 4, 3, 2
파이썬을 이용해 이 데이터의 중앙값을 찾아보자. 대부분의 사람들이 이 점수의 평균이 정당하다고 주장할 것이다. 하지만, 평균을 수학적으로 실행할 수 없는 이유는 두 점수를 빼거나 더했을 때, 예를 들어 4점에서 2점을 빼면 두 점수 차이가 실제로 아무 의미를 나타내지 못하기 때문이다. 점수 사이에서 더하기/빼기가 의미가 없다면 평균도 의미가 없다.

등간수준
등간 수준에서는 좀 더 정량화된 데이터를 사용하고 복잡한 수학공식이 허용된다. 서열수준과 등간 수준의 기본적인 차이는 뺄셈의 허용여부다.
예제
온도는 등간 수준 데이터의 훌륭한 예다. 텍사스가 화씨 100도 터키 이스탄불이 화씨 80도인 경우 텍사스는 이스탄불보다 20도 더 따뜻하다.
1~5를 척도로 사용하는 설문조사의 서열 수준 데이터의 경우 뺄셈의 의미가 없는 것처럼, 등간수준의 데이터와 구분해서 사용할 수 있도록 하자.
허용된 수학
- 더하기
- 빼기
등간수준의 데이터는 이 두가지 연산을 허용하므로써 완전히 새로운 방식으로 데이터를 이야기할 수 있게 된다.
중심의 측정
등간수준에서는 중앙값과 최빈수를 사용해 이 데이터를 설명할 수 있다. 그러나 일반적으로 데이터 중심의 가장 정확한 설명은 산술 평균 Arithmaetic mean으로 일반적으로 간단히 평균이라고 말하는 것이다. 평균의 정의는 모든 측정값을 합칠 수 있어야 평균을 구할 수가 있다. 서열수준까지는 더하기가 의미가 없었고, 평균에서 의미를 구할 수 없었다.
제약회사에서 새로운 백신을 담고 있는 냉장고의 온도를 살펴보자.
매 시간마다 다음과 같은 데이터 포인트로 온도를 측정한다.

편차의 측정
데이터의 중심에 대해서 이야기하기도 하지만, 데이터 과학에서는 데이터를 펼치는 방법에 대해 이야기하는 것이 매우 중요하다. 이 현상을 설명하는 측정을 편차 측정 (Measures of Variation) 이라고 한다. 이 개념은 매우 중요하다.
표준편차 : 데이터가 어떻게 퍼져 있는가를 나타내는 숫자
중심측정과 표준편차 두 가지 개념만으로도 데이터셋을 거의 완전하게 설명할 수 있다.
등간수준에서의 표준편차는 데이터 변동성의 가장 일반적인 척도다.
표준편차는 평균값으로부터 데이터 포인트까지의 평균거리로 생각할 수 있다. 수학적으로 옳은 설명은 아니지만, 이해하기 쉽게 설명하면 그렇다.
표준편차 구하는 방법
- 데이터의 평균을 구한다.
- 데이터셋의 각 숫자에 대해 평균에서 숫자를 빼고 그것을 제곱한다.
- 각 제곱 차이의 평균을 구한다.
- 3단계에서 얻은 수의 제곱근을 취한다. 이것이 표준편차다.
import numpy as np
temps = [31, 32, 32, 31, 28, 29, 31, 38, 32, 31, 30, 31, 26]
mean = np.mean(temps)
squared_differences = [] # 차이를 제곱한 빈 목록
for temperature in temps:
difference = temperature - mean # 특정 포인트와 평균과의 거리
squared_difference = difference**2 # 차이를 제곱한다.
squared_differences.append(squared_difference) # 이것을 목록에 추가한다.
average_squared_difference = np.mean(squared_differences) # 이 숫자를 분산이라고 부른다.
standard_deviation = np.sqrt(average_squared_difference)
print(standard_deviation)이 코드의 결과값으로 보면, 데이터셋의 표준편차가 약 2.6이고, 평균적으로 데이터 포인트가 약 31의 평균 온도로부터 2.6도 떨어져 있음을 알려준다. 이는 평균 기온이 조만간 다시 29도 이하로 떨어질 수 있다는 의미다.
이러한 편차의 측정은 데이터가 어떻게 퍼져 나가고 분산됐는지에 대한 매우 명확한 그림을 제공한다.
표준편차를 아는 것은 데이터의 범위와 데이터가 어떻게 움직일 수 있는지에 관심이 있는 경우에 특히 중요하다.
등간수준의 데이터에서는 자연적인 0이라는 것이 없다.
비율수준
비율수준은 수학적 연산이 가장 강력하게 적용될 수 있는 데이터 수준이다. 비율 수준은 순서와 차이를 저으이할 수 있을 뿐만 아니라, 곱하기와 나누기를 허용한다.
은행에 있는 돈은 비율수준 데이터다. 은행에 돈이 없음인 경우도 있고, $2가 $1보다 2배 많음을 의미하는 경우다.
중심의 측정
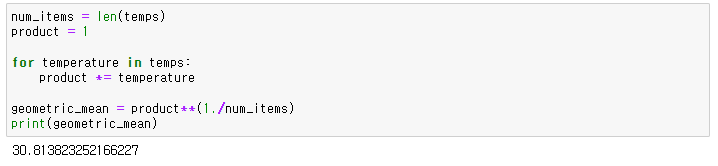
기하평균 : 산술평균이 모든 합의 평균이라면, 기하평균은 모든 곱의 평균이다
'Mathematics > Statistics' 카테고리의 다른 글
| 데이터 과학 수행의 5가지 필수 단계 (0) | 2022.01.09 |
|---|---|
| 데이터셋을 만날 때마다 해야 하는 질문 (0) | 2022.01.09 |
| 팀 버너스 리의 월드 와이드 웹 (0) | 2021.12.31 |
| 결측치(Missing Value)란? (0) | 2021.12.31 |
| 회귀분석(regression analysis)이란? (0) | 2021.12.30 |